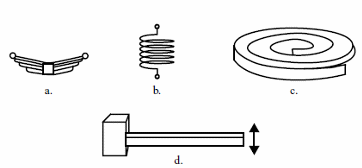
(a) flat
(b) spiral
(c) helical
(d) torsion
Properties:
a) Springs can store energy
b)Common types are made with steel , phosphor bronze, brass and other alloys
Formulas
a) Spring Rate - constant (figure 2.24)
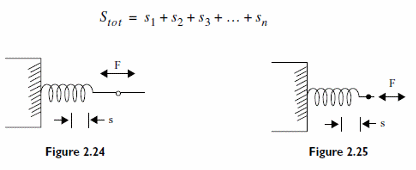
R = F/S
Where:
R is the spring rate
F is the applied force
S is deformation
Obs: General characteristic is given by R = dF/ds
b) Spring Work - constant (figure 2.25)
W = F x (S/2)
Where:
W is the work in joules
s is the deformation in meters
F is the force in Newtons
Obs: the general characteristic is given by: W =?F.ds
Springs in series and Parallel
As shown by figure 3 springs can be used in series and parallel (with an analogy with resistors and capacitors)
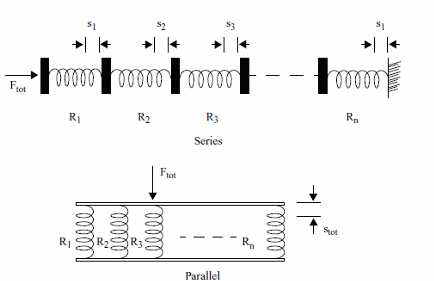
Formulas
a) Springs in series
Stot = s1 + s2 + s3 + ......+ sn
Ftot = F1 = F2 = F3 = ..... = Fn (f2.41.b)
Rtot = R1 + R2 + R3 + ..... + Rn (f2.41.c)
Where:
Stot, s1, s2, s3, sn are the deformations
Ftot, F1, F2, F3, Fn are the involved forces
Rtot, R1, R2, R3, Rn are the spring rates
b) Springs in parallel
Stot = S1 = S2 = S3 = ...... = Sn
Ftot = F1 + F2 + F3 + .... + Fn
1/Rtot = 1/R1 + 1/R2 + 1/R3 + ..... + 1/Rn
Obs: formulas valid for compression and tension
How to determine the characteristics of a spring
Figure 4 shows simple processes to determine the characteristics of a spring.
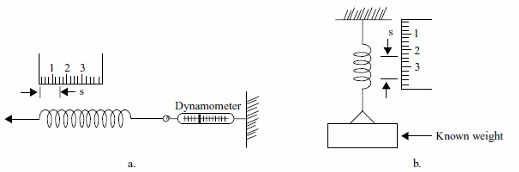
(a) using a dynamometer
(b) Using known weights



